hamming-distance

The Hamming distance between two integers is the number of positions at which the corresponding bits are different.

Given two integers x and y, calculate the Hamming distance.

Note: 0 ≤ x, y < 231.

Example:

Input: x = 1, y = 4

Output: 2

Explanation:
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑

The above arrows point to positions where the corresponding bits are different.

Consideration

This problem is also have a relationship with ‘^’ , Think about it :

1(0001) and 4(0100) their Xor is 5(0101) . next we use & Operator to calculate the number of 1 , let the binary & 1 ,if result is 1 ,sum’s up , use » to move the postion.

5(0101)
0&1  = 0            pass
01&01 = 1           sum
010&001 = 0         pass
0101&0001 = 1       sum

so,the anwser is 2

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
 public int hammingDistance(int x, int y) {
	         
         int sum = 0;
         int xor = x ^ y;
	 
	    for(int i = 0;i<32;i++){
	    	
             sum+=(xor>>i)&1;
	    }
	       
		return sum;
	    }
}

tips: if you don’t understand the Xor ,you can see my older article which about Xor .and the flowing is about Hamming Distance from wiki.

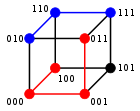
3-bit binary cube for finding Hamming distance

Two example distances: 100→011 has distance 3; 010→111 has distance 2

The minimum distance between any two vertices is the Hamming distance between the two binary strings.